文章

Paper | LST

发表于
作者 MiaoHN
6 分钟阅读
Paper | LST
  • Title: Ladder Side-Tuning for Parameter and Memory Efficient Transfer Learning
  • Authors: Yi-Lin Sung, Jaemin Cho, Mohit Bansal
  • Publish: NeurIPS 2022
  • Urls: Paper, GitHub

1. Introduction

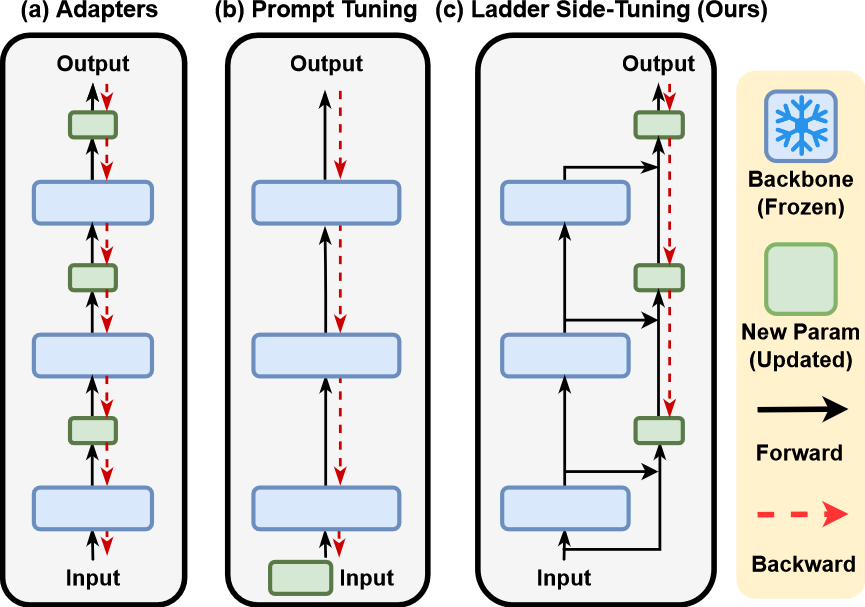
当前，对 transformer 进行大规模预训练和 fine-tuning 已经得到了广泛的应用。模型的尺寸增长很快，对参数集进行 fine-tuning 也成为一笔不小的开销。Parameter-efficient transfer learning (PETL) 是近期兴起的一个研究方向，它的任务是设计一个系统，使得针对不同的任务无需训练整个模型就能达到很好的效果。在 NLP、CV 以及 VL 中，有两种主要的 PETL 方式，如图 1 的 (a)，(b) 所示：

图 1. 不同的迁移学习方式：(a) Adapters，(b) Prompt Tuning，(c) Ladder Side-Tuning(LST).

虽然这些 PETL 方法减少了需要更行的参数数量，但它们对训练时内存需求的减少最多只有 30%，使得它们无法应用于许多计算资源有限的实际应用场景中。

模型在训练时要记录每个可更新参数的梯度以及进行反向传播，所以需要额外的内存空间。

基于这些问题，本文提出了 Ladder Side-Tuning（LST），该方法将可训练参数从主干模型中分离为 side network，进而使整个模型适应新任务。如图 1 的 (c) 所示，LST 大致有如下几个特点：

  1. LST 并不在预训练模型中添加可学习参数，从而完全消除大型骨干网络昂贵的反向传播需要，并在 transfer learning 期间节省大量内存。
  2. 在对 side network 进行初始化时，利用网络剪枝技术来检索较小的剪枝网络并将其用作 side network，同时减少网络层数来提高 LST 的效率。
  3. 因为主干网络和 side network 可以并行计算，所以在推理过程中 LST 也不一定会使用更多的推理时间。

3. Ladder Side-Tuning (LST)

3.1 Dependency on Backpropagation through Large Backbone Model

首先考虑一个 $N$ 层的多层感知机（MLP）：$f_N(f_{N-1}(\dots f_2(f_1(x))\dots))$，这里 $f_i(x)=\sigma_i(W_ix+b_i)$。将第 $i$ 层的输出记为 $a_{i+1}$，激活前的值为 $z_{i+1}$，即 $a_{i+1}=\sigma_i(z_{i+1})$。对损失 $L$ 进行反向传播时，有

\[\frac{\partial L}{dW_i}=\frac{\partial L}{\partial a_{i+1}}\frac{\partial a_{i+1}}{\partial z_{i+1}}\frac{\partial z_{i+1}}{\partial W_i}=\frac{\partial L}{\partial a_{i+1}}\sigma_i^\prime a_i,\quad \frac{\partial L}{db_i}=\frac{\partial L}{\partial a_{i+1}}\sigma_i^\prime\]

于是 $a_i$ 的梯度 $\frac{\partial L}{\partial a_{i+1}}$ 可以通过 $a_{i+2}$ 通过链式规则得到：

\[\frac{\partial L}{\partial a_{i+1}}=\frac{\partial L}{\partial a_{i+2}}\frac{\partial a_{i+2}}{\partial z_{i+2}}\frac{\partial z_{i+2}}{\partial a_{i+1}}=\frac{\partial L}{\partial a_{i+2}}\sigma_{i+1}^\prime W_{i+1}\]

对这两个式子进行观察，可以发现有两个变量影响内存占用：

  1. $\{a\}$ 对应于更新后的参数 $\{W\}$
  2. $\{\sigma^\prime\}$ 必须针对链式法则进行缓存

现有的 PETL 方法，比如 Adapters1、LoRA2、Prompt-tuning3 以及 BitFit4 都是通过减小 $\lvert a\rvert$ 来减少可更新参数 $\{W\}$，进而降低内存占用。

由于大部分的方法都不改变维度（$\lvert a\rvert=\lvert\sigma^\prime\rvert$），反向传播的内存占用 $\lvert a\rvert+\lvert\sigma^\prime\rvert$ 在只改变 $\lvert a\rvert$ 的情况下最多减少 50%。

3.2 Ladder Side Network for Transformers

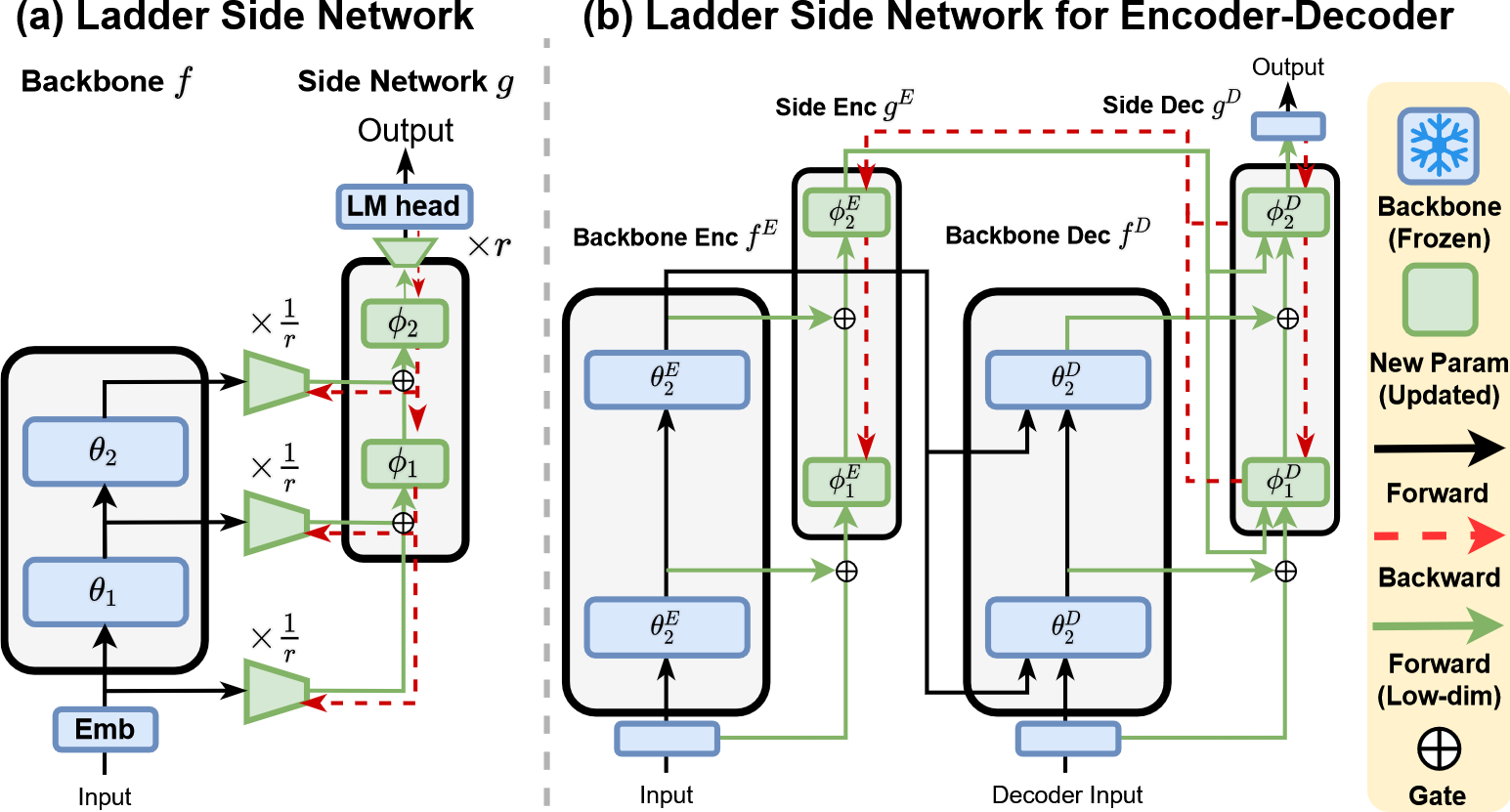
图 2. 带有 transformers 的 LST.

本文提出的 ladder side network 是一个小型且独立的网络，将主干 transformer 的中间激活作为输入并进行预测。注意 LST 方法并不限于特定的结构。图 2(a) 展示编码器结构的 LST，图 2(b) 展示具有编码器-解码器结构的 LST。

  • Lightweight architecture. side network $g$ 是主干 transformer $f$ 的轻量版本，$g$ 中所有权重和隐藏状态是 $f$ 的 $\frac{1}{r}$ 倍，这里 $r$ 是缩减因子（$r=2,4,8,16$）。通过轻量化的操作，使得内存占用变为 $\frac{\lvert a\rvert+\lvert\sigma^\prime\rvert}{r}$，使得 LST 比其他 PETL 方法拥有更好的内存效率。
  • Get ladder connections. 在实验中文章发现，late fusion 损害 transformer 架构在 NLP 任务中的性能。为了解决该问题，本文使用从 $f$ 到 $g$ 的中间激活的 shortcut connection（称为 ladder），首先对中间激活进行下采样，$g$ 中的每一个 transformer layer 将 backbone 的 $h_i^f$ 与 side network 的上一层输出 $h_{i-1}^g$ 通过学习门控 $\mu_i*h_i^f+(1-\mu_i)*h_{i-1}^g$ 来结合，这里 $\mu_i=\text{sigmoid}(\frac{\alpha_i}{T})$ 是一个零初始化可学习标量 $\alpha_i$ 以及 $T(=0.1)$ 组成的门控。

3.3 Structural Weight Initialization for Ladder Side Network

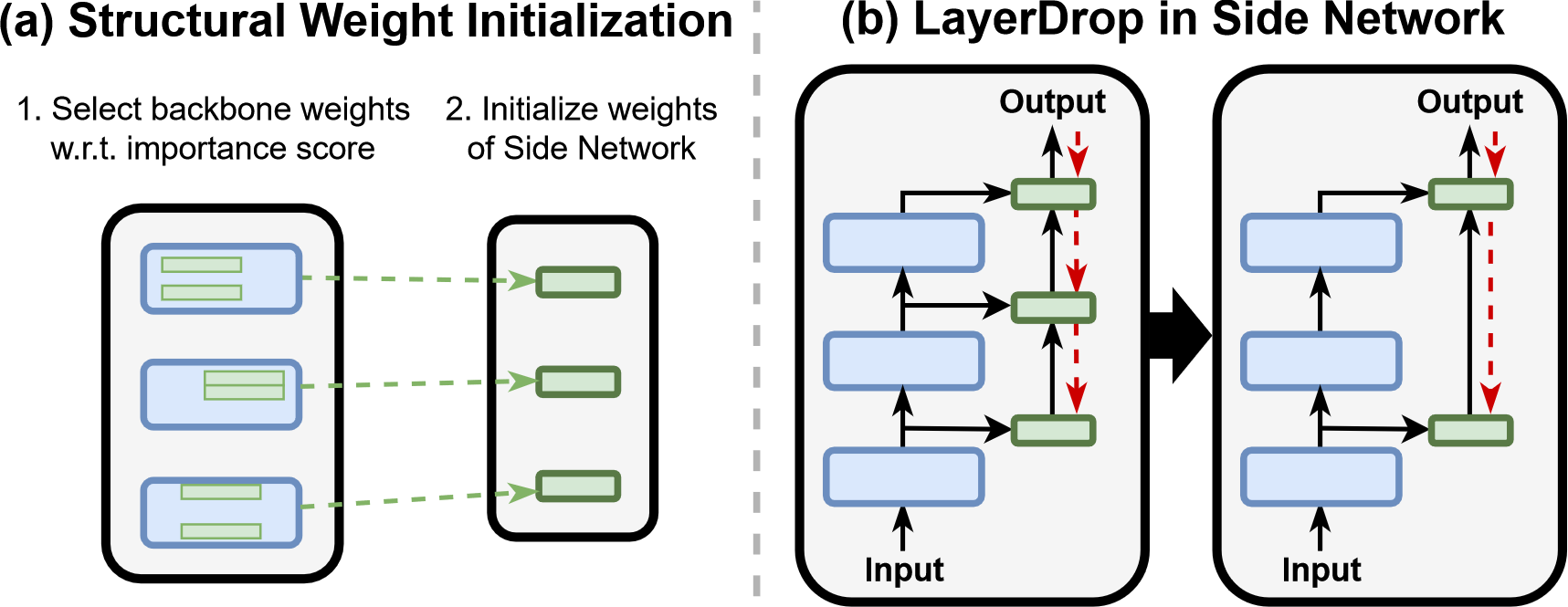
图 3. (a) Structural Weight Initialization；(b) Layer Dropping.

文章发现使用主干网络 $\theta$ 的结构剪枝5对初始化 side network $\phi$ 很有帮助，如图 3(a) 所示。给定一个主干网络的矩阵 $W\in\mathbb{R}^{d_{out}\times d_{in}}$ 和权重的重要性矩阵 $I\in\mathbb{R}^{d_{out}\times d_{in}}$：

  1. 首先计算每行的重要性分数 $s_i=\sum_j\lvert I_{i,j}\rvert$
  2. 然后在 $W$ 中选择 $\frac{d_{out}}{r}$ 个有最大重要性分数的行，修剪剩余的行以获得新的权重矩阵 $W^P\in\mathbf{R}^{\frac{d_{out}}{r}\times d_{in}}$

  1. Neil Houlsby et al. Parameter-efficient transfer learning for nlp. PMLR, 2019. ↩︎

  2. Edward J. Hu et al. Lora: Low-rank adaptation of large language models. CoRR, 2021. ↩︎

  3. Brian Lester et al. The power of scale for parameter-efficient prompt tuning. EMNLP, 2021. ↩︎

  4. Elad Ben Zaken et al. Bitfit: Simple parameter-efficient fine-tuning for transformer-based masked language-models. CoRR, 2021. ↩︎

  5. Hao Li et al. Pruning filters for efficient convnets. ICLR, 2017. ↩︎

Paper Reading
paper
本文由作者按照 CC BY 4.0 进行授权