密钥交换算法

DH 密钥交换

DH 密钥交换，全称 Diffie-Hellman key exchange，它可以让双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥，这个密钥可以在后续的通讯中作为对称密钥来加密通讯内容。其原理使用了数论中的一个简单的推论，从理论上保证了其加密的可靠性。虽然如此，DH 密钥交换并不是完全安全的，攻击人可能会通过中间人通讯进行攻击，可以说用心险恶

The system…has since become known as Diffie–Hellman key exchange. While that system was first described in a paper by Diffie and me, it is a public key distribution system, a concept developed by Merkle, and hence should be called ‘Diffie–Hellman–Merkle key exchange’ if names are to be associated with it. I hope this small pulpit might help in that endeavor to recognize Merkle’s equal contribution to the invention of public key cryptography.

– Martin Edward Hellman¹

虽然 DH 密钥交换算法的雏形是 Hellman 和 Diffie 两个人先在一篇论文中先提出的，但是该算法的概念是 Merkle 提出的。所以当事人 Hellman 实际上觉得这个算法应该为 DHM 算法

算法描述

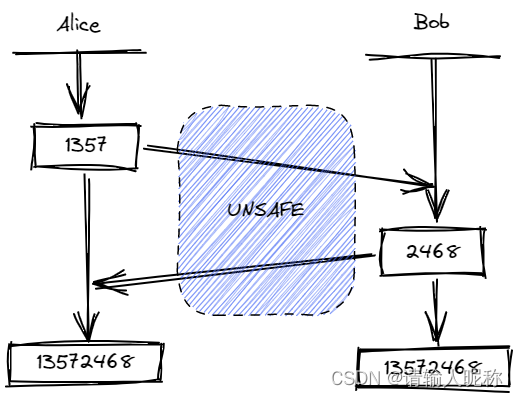
我们考虑一个简单的情景：Alice 和 Bob 在不安全的信道上发送密文，首先需要一个统一的密码，也就是密钥。由于信道不安全，不能直接将密钥明文从信道上发送。此时有一个简单的策略：Alice 决定要交换密钥时，她会将密码的前一半“1357”通过中间的同学交给 Bob，Bob 收到后知道该更改密码了，于是他将“2468”写到纸条上送回 Alice。本次交换设置的新公钥就是“13572468”。

这个算法是有漏洞的：如果中间的用户稍加留意，他也可以同时得到上面的两个密钥段，也就是知道了密钥。那么这个办法就不可行了吗？也不尽然，既然中间的用户可以看到他们发的内容，那就需要一个巧妙的方法将密钥“隐藏”到一个运算中。Alice 和 Bob 需要一个办法，通过二者交换一次数据，就能各自算出密码，这个办法就是 DH 算法。

实际上 DH 算法用到的数论知识并不多，但确实好用，只用到了同余以及离散对数这个公认难解的数学问题。先留个感性印象，对任意一个正整数 $x$，先对它求 $a$ 次幂再求 $b$ 次幂得到的值，与先求 $b$ 次幂再求 $a$ 次幂得到的值相同，其实就是 $(x^a)^b=(x^b)^a$，如果每次在求幂的时候对一个素数取余，那么等式应该也是成立的，即 $(x^a(mod\ p))^b(mod\ p)=(x^b(mod\ p))^a(mod\ p)$（后面有证明）。两人将密钥交换过程设计为：

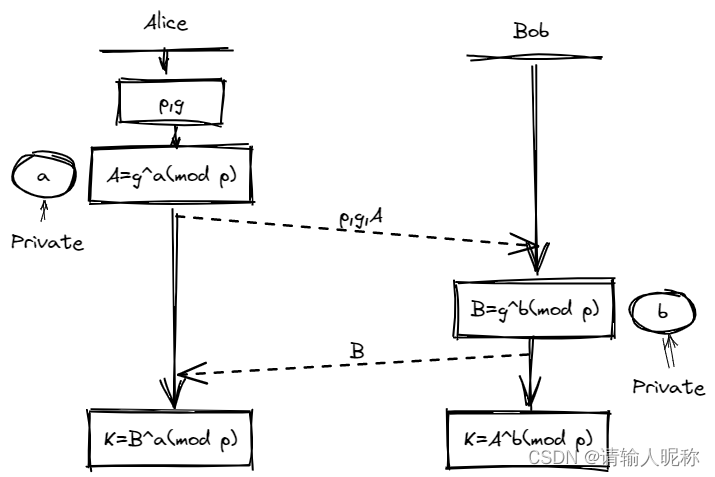
算法步骤：

1. Alice 选择一个质数 $p$ 以及一个生成元 $g$
2. Alice 偷偷设置一个只有自己知道的数 $a$，计算出 $A=g^a(mod\ p)$ 后将 $g,p,A$ 都交给 Bob
3. Bob 设置一个只有自己知道的数 $b$，求出 $B=g^b(mod\ p)$ 后将 $B$ 发送给 Alice
4. 此时 Alice 可以通过 $K=B^a(mod\ p)$ 得到密码，Bob 可以通过 $K=A^b(mod\ p)$ 得到密码

离散对数：

可以看到，如果中间的同学偷看内容，只能知道 $p,g,A,B$ 这四个数的内容。而仅靠这四个数很难求得最终的 $K$。要想得到 $K$，则必须得到 $a$ 和 $b$ 中的最少一个值，获得这两个数的难度都很大：如果想要得到 $a$，因为 $A=g^a(mod\ p)$，按照指数的写法，$a$ 可以写成 $a=\log_gA(mod\ p)$，这是一个标准的离散对数，求解难度极高²，目前也么有有效的通用算法。

证明过程：

通过整个实现过程，其实就是证明，$(g^b(mod\ p))^a(mod\ p)$ 是否等于 $(g^a(mod\ p))^b(mod\ p)$，可以转为证明 $(g^b(mod\ p))^a(mod\ p)=g^{ab}(mod\ p)$，观察这个式子，其实我们只需要证明

\[(x(mod\ p))^a(mod\ p)=x^a(mod\ p)\]

上面的式子可以用带余除法的式子强行证出来。首先令

\[x=qp+r\]

再通过二项式展开的公式可以得到：

\[\begin{aligned} x^a(mod\ p) =&(qp+r)^a(mod\ p)\\\\ =&\sum_{i=0}^aC_a^i(qp)^ir^{a-i}\\\\ =&r^a(mod\ p)\\\\ =&(x(mod\ p))^a(mod\ p) \end{aligned}\]

原式得证。上面就是 DH 密钥交换算法的实现原理。

缺陷

计算性能不佳：后面通过椭圆曲线（ECC）解决了这一问题，也就是ECDH

你可能还知道中间人攻击这个词，实际上密钥交换算法与中间人攻击两个不同的方向，单纯的密钥交换无法是无法判断中间人的。要想防范中间人攻击，还需要配合认证等手段。

DHE 算法

DH 密钥交换算法的原理在前面已经说明，在实际情况中，根据私钥生成的方式将 DH 算法再分为两类³：

• static DH 算法
• DHE 算法

static DH 算法中，总有一方的私钥是静态的，比如服务器方的 $a$ 是不变的，客户端的私钥是随机的。这种情况下，攻击者可以先截获大量密文，然后通过暴力破解服务器方的私钥，一旦破解，之前所有的密文都会被破解。所以我们可以说 static DH 不具备前向安全性

因为 static DH 的静态私钥可能会被破解，所以将其改为双方每次在密钥交换时随机生成自己的私钥，这就是 DHE 算法。DHE 算法的全称是 Diffie-Hellman Ephemeral key exchange，Ephemeral 是临时的意思。

ECDH 算法

DH 算法虽然可以用，但是计算比较复杂，性能较低。ECDH 算法全称为 Elliptic Curve Diffie-Hellman key exchange，这个算法通过使用椭圆曲线密码学（ECC）来降低密钥的计算量，得到了广泛的使用。

椭圆曲线密码学：

针对密码学应用上的椭圆曲线是在有限域（不是实数域）上的平面曲线，表达式为⁴

\[y^2=x^3+ax+b\]

考虑 $K=kG$，其中 $K,G$ 为椭圆曲线 $E_p(a,b)$上的点，$n$ 为 $G$ 的阶，$k$ 为小于 $n$ 的整数。则给定 $k$ 和 $G$，根据加法法则，计算 $K$ 很容易。但如果反过来，给定 $K$ 和 $G$，求 $k$ 就非常困难。因为实际使用中的 ECC 原则上把 $p$ 取得相当大，$n$ 也相当大，要把 $n$ 个解点逐一算出来列成上表是不可能的。这就是椭圆曲线加密算法的数学依据

算法流程：

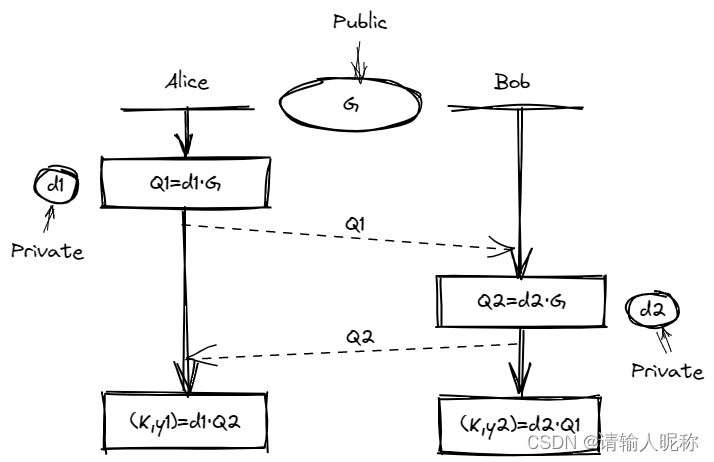
ECDH 算法的大体步骤和 DH 算法基本一样，只是在计算时使用了椭圆曲线的性质

• 双方事先确定好使用哪种椭圆曲线，和曲线上的基点 $G$，这两个参数都是公开的
• 双方各自随机生成一个随机数作为私钥 $d$，并与基点 $G$ 相乘得到公钥 $Q=dG$，此时小红的公私钥为 $Q_1$ 和 $d_1$，小明的公私钥为 $Q_2$ 和 $d_2$
• 双方交换各自的公钥，最后小红计算点 $(x_1,y_1)=d_1Q_2$，小明计算点 $(x_2,y_2)=d_2Q_1$，由于椭圆曲线上是可以满足乘法交换和结合律，所以 $d_1Q_2=d_1d_2G=d_2d_1G=d_2Q_1$，因此双方的 $x$ 坐标是一样的，所以它是共享密钥，也就是会话密钥

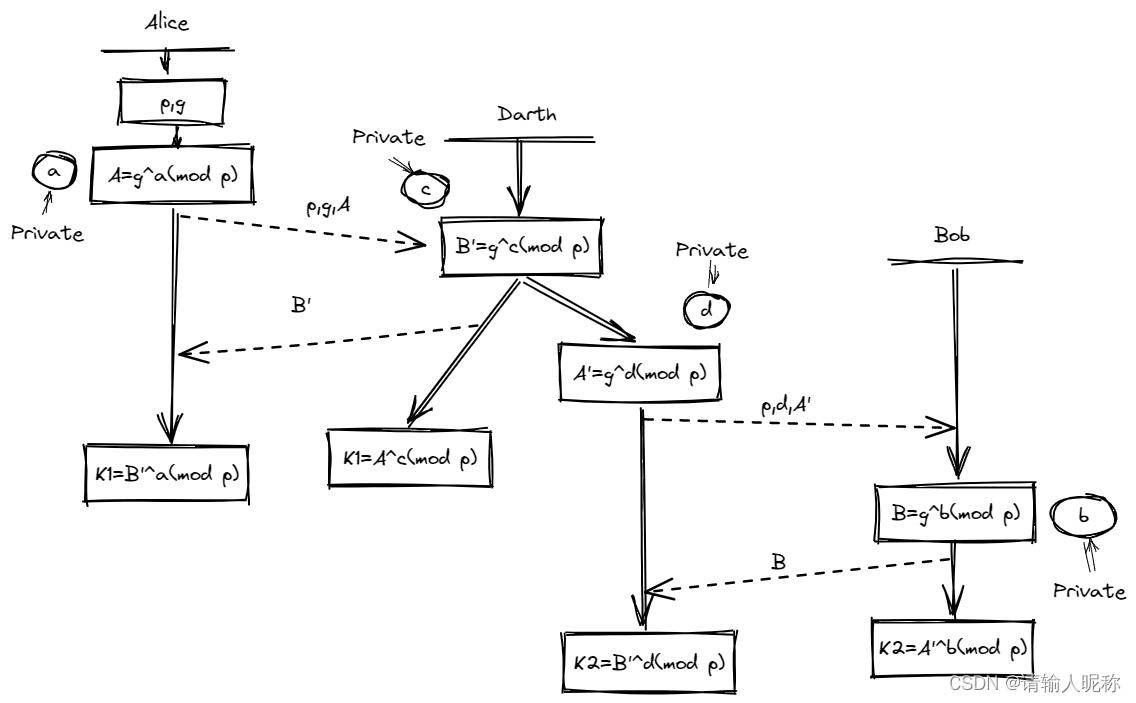
中间人攻击⁵

密钥交换算法无法方法中间人攻击，这两个概念都不在一个范畴，以 DH 算法的中间人攻击为例，其过程可能为：

1. An Overview of Public Key Cryptography ↩︎

2. 证明与计算(2): 离散对数问题(Discrete logarithm Problem, DLP) ↩︎

3. 图解 ECDHE 密钥交换算法 ↩︎

4. ECC 椭圆曲线详解(有具体实例) ↩︎

5. 中间人攻击 ↩︎